Dunn Index

Module Interface

class torchmetrics.clustering.DunnIndex(p=2, **kwargs)

Compute Dunn Index.

\[DI_m = \frac{\min_{1\leq i<j\leq m} \delta(C_i,C_j)}{\max_{1\leq k\leq m} \Delta_k}\]

Where \(C_i\) is a cluster of tensors, \(C_j\) is a cluster of tensors, and \(\delta(C_i,C_j)\) is the intercluster distance metric for \(m\) clusters.

This clustering metric is an intrinsic measure, because it does not rely on ground truth labels for the evaluation. Instead it examines how well the clusters are separated from each other. The score is higher when clusters are dense and well separated, which relates to a standard concept of a cluster.

As input to forward and update the metric accepts the following input:

• data (Tensor): float tensor with shape (N,d) with the embedded data. d is the dimensionality of the embedding space.

• labels (Tensor): single integer tensor with shape (N,) with cluster labels

As output of forward and compute the metric returns the following output:

• dunn_index (Tensor): A tensor with the Dunn Index

Parameters:

kwargs (Any) – Additional keyword arguments, see Advanced metric settings for more info.

Example::

>>> import torch
>>> from torchmetrics.clustering import DunnIndex
>>> data = torch.tensor([[0, 0], [0.5, 0], [1, 0], [0.5, 1]])
>>> labels = torch.tensor([0, 0, 0, 1])
>>> dunn_index = DunnIndex(p=2)
>>> dunn_index(data, labels)
tensor(2.)

plot(val=None, ax=None)

Plot a single or multiple values from the metric.

Parameters:

• val (Union[Tensor, Sequence[Tensor], None]) – Either a single result from calling metric.forward or metric.compute or a list of these results. If no value is provided, will automatically call metric.compute and plot that result.

• ax (Optional[Axes]) – An matplotlib axis object. If provided will add plot to that axis

Return type:

tuple[Figure, Union[Axes, ndarray]]

Returns:

Figure and Axes object

Raises:

ModuleNotFoundError – If matplotlib is not installed

>>> # Example plotting a single value
>>> import torch
>>> from torchmetrics.clustering import DunnIndex
>>> data = torch.tensor([[0, 0], [0.5, 0], [1, 0], [0.5, 1]])
>>> labels = torch.tensor([0, 0, 0, 1])
>>> metric = DunnIndex(p=2)
>>> metric.update(data, labels)
>>> fig_, ax_ = metric.plot(metric.compute())

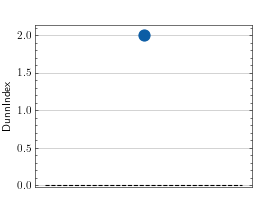
>>> # Example plotting multiple values
>>> import torch
>>> from torchmetrics.clustering import DunnIndex
>>> metric = DunnIndex(p=2)
>>> values = [ ]
>>> for _ in range(10):
...     values.append(metric(torch.randn(50, 3), torch.randint(0, 2, (50,))))
>>> fig_, ax_ = metric.plot(values)

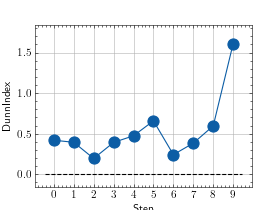
Functional Interface

torchmetrics.functional.clustering.dunn_index(data, labels, p=2)

Compute the Dunn index.

Parameters:

• data (Tensor) – feature vectors

• labels (Tensor) – cluster labels

• p (float) – p-norm used for distance metric

Return type:

Tensor

Returns:

scalar tensor with the dunn index

Example

>>> from torchmetrics.functional.clustering import dunn_index
>>> data = torch.tensor([[0, 0], [0.5, 0], [1, 0], [0.5, 1]])
>>> labels = torch.tensor([0, 0, 0, 1])
>>> dunn_index(data, labels)
tensor(2.)