Cohen Kappa¶
Module Interface¶
- class torchmetrics.CohenKappa(**kwargs)[source]¶
Calculate Cohen’s kappa score that measures inter-annotator agreement.
\[\kappa = (p_o - p_e) / (1 - p_e)\]where \(p_o\) is the empirical probability of agreement and \(p_e\) is the expected agreement when both annotators assign labels randomly. Note that \(p_e\) is estimated using a per-annotator empirical prior over the class labels.
This function is a simple wrapper to get the task specific versions of this metric, which is done by setting the
taskargument to either'binary'or'multiclass'. See the documentation ofBinaryCohenKappaandMulticlassCohenKappafor the specific details of each argument influence and examples.- Legacy Example:
>>> from torch import tensor >>> target = tensor([1, 1, 0, 0]) >>> preds = tensor([0, 1, 0, 0]) >>> cohenkappa = CohenKappa(task="multiclass", num_classes=2) >>> cohenkappa(preds, target) tensor(0.5000)
BinaryCohenKappa¶
- class torchmetrics.classification.BinaryCohenKappa(threshold=0.5, ignore_index=None, weights=None, validate_args=True, **kwargs)[source]¶
Calculate Cohen’s kappa score that measures inter-annotator agreement for binary tasks.
\[\kappa = (p_o - p_e) / (1 - p_e)\]where \(p_o\) is the empirical probability of agreement and \(p_e\) is the expected agreement when both annotators assign labels randomly. Note that \(p_e\) is estimated using a per-annotator empirical prior over the class labels.
As input to
forwardandupdatethe metric accepts the following input:preds(Tensor): A int or float tensor of shape(N, ...). If preds is a floating point tensor with values outside [0,1] range we consider the input to be logits and will auto apply sigmoid per element. Additionally, we convert to int tensor with thresholding using the value inthreshold.target(Tensor): An int tensor of shape(N, ...).
Tip
Additional dimension
...will be flattened into the batch dimension.As output to
forwardandcomputethe metric returns the following output:bc_kappa(Tensor): A tensor containing cohen kappa score
- Parameters:
threshold¶ (
float) – Threshold for transforming probability to binary (0,1) predictionsignore_index¶ (
Optional[int]) – Specifies a target value that is ignored and does not contribute to the metric calculationweights¶ (
Optional[Literal['linear','quadratic','none']]) –Weighting type to calculate the score. Choose from:
Noneor'none': no weighting'linear': linear weighting'quadratic': quadratic weighting
validate_args¶ (
bool) – bool indicating if input arguments and tensors should be validated for correctness. Set toFalsefor faster computations.kwargs¶ (
Any) – Additional keyword arguments, see Advanced metric settings for more info.
- Example (preds is int tensor):
>>> from torch import tensor >>> from torchmetrics.classification import BinaryCohenKappa >>> target = tensor([1, 1, 0, 0]) >>> preds = tensor([0, 1, 0, 0]) >>> metric = BinaryCohenKappa() >>> metric(preds, target) tensor(0.5000)
- Example (preds is float tensor):
>>> from torchmetrics.classification import BinaryCohenKappa >>> target = tensor([1, 1, 0, 0]) >>> preds = tensor([0.35, 0.85, 0.48, 0.01]) >>> metric = BinaryCohenKappa() >>> metric(preds, target) tensor(0.5000)
- plot(val=None, ax=None)[source]¶
Plot a single or multiple values from the metric.
- Parameters:
val¶ (
Union[Tensor,Sequence[Tensor],None]) – Either a single result from calling metric.forward or metric.compute or a list of these results. If no value is provided, will automatically call metric.compute and plot that result.ax¶ (
Optional[Axes]) – An matplotlib axis object. If provided will add plot to that axis
- Return type:
- Returns:
Figure object and Axes object
- Raises:
ModuleNotFoundError – If matplotlib is not installed
>>> from torch import rand, randint >>> # Example plotting a single value >>> from torchmetrics.classification import BinaryCohenKappa >>> metric = BinaryCohenKappa() >>> metric.update(rand(10), randint(2,(10,))) >>> fig_, ax_ = metric.plot()
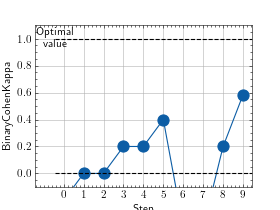
>>> from torch import rand, randint >>> # Example plotting multiple values >>> from torchmetrics.classification import BinaryCohenKappa >>> metric = BinaryCohenKappa() >>> values = [ ] >>> for _ in range(10): ... values.append(metric(rand(10), randint(2,(10,)))) >>> fig_, ax_ = metric.plot(values)
MulticlassCohenKappa¶
- class torchmetrics.classification.MulticlassCohenKappa(num_classes, ignore_index=None, weights=None, validate_args=True, **kwargs)[source]¶
Calculate Cohen’s kappa score that measures inter-annotator agreement for multiclass tasks.
\[\kappa = (p_o - p_e) / (1 - p_e)\]where \(p_o\) is the empirical probability of agreement and \(p_e\) is the expected agreement when both annotators assign labels randomly. Note that \(p_e\) is estimated using a per-annotator empirical prior over the class labels.
As input to
forwardandupdatethe metric accepts the following input:preds(Tensor): Either an int tensor of shape(N, ...)` or float tensor of shape ``(N, C, ..). If preds is a floating point we applytorch.argmaxalong theCdimension to automatically convert probabilities/logits into an int tensor.target(Tensor): An int tensor of shape(N, ...).
Tip
Additional dimension
...will be flattened into the batch dimension.As output to
forwardandcomputethe metric returns the following output:mcck(Tensor): A tensor containing cohen kappa score
- Parameters:
num_classes¶ (
int) – Integer specifying the number of classesignore_index¶ (
Optional[int]) – Specifies a target value that is ignored and does not contribute to the metric calculationweights¶ (
Optional[Literal['linear','quadratic','none']]) –Weighting type to calculate the score. Choose from:
Noneor'none': no weighting'linear': linear weighting'quadratic': quadratic weighting
validate_args¶ (
bool) – bool indicating if input arguments and tensors should be validated for correctness. Set toFalsefor faster computations.kwargs¶ (
Any) – Additional keyword arguments, see Advanced metric settings for more info.
- Example (pred is integer tensor):
>>> from torch import tensor >>> from torchmetrics.classification import MulticlassCohenKappa >>> target = tensor([2, 1, 0, 0]) >>> preds = tensor([2, 1, 0, 1]) >>> metric = MulticlassCohenKappa(num_classes=3) >>> metric(preds, target) tensor(0.6364)
- Example (pred is float tensor):
>>> from torchmetrics.classification import MulticlassCohenKappa >>> target = tensor([2, 1, 0, 0]) >>> preds = tensor([[0.16, 0.26, 0.58], ... [0.22, 0.61, 0.17], ... [0.71, 0.09, 0.20], ... [0.05, 0.82, 0.13]]) >>> metric = MulticlassCohenKappa(num_classes=3) >>> metric(preds, target) tensor(0.6364)
- plot(val=None, ax=None)[source]¶
Plot a single or multiple values from the metric.
- Parameters:
val¶ (
Union[Tensor,Sequence[Tensor],None]) – Either a single result from calling metric.forward or metric.compute or a list of these results. If no value is provided, will automatically call metric.compute and plot that result.ax¶ (
Optional[Axes]) – An matplotlib axis object. If provided will add plot to that axis
- Return type:
- Returns:
Figure object and Axes object
- Raises:
ModuleNotFoundError – If matplotlib is not installed
>>> from torch import randn, randint >>> # Example plotting a single value >>> from torchmetrics.classification import MulticlassCohenKappa >>> metric = MulticlassCohenKappa(num_classes=3) >>> metric.update(randn(20,3).softmax(dim=-1), randint(3, (20,))) >>> fig_, ax_ = metric.plot()
>>> from torch import randn, randint >>> # Example plotting a multiple values >>> from torchmetrics.classification import MulticlassCohenKappa >>> metric = MulticlassCohenKappa(num_classes=3) >>> values = [] >>> for _ in range(20): ... values.append(metric(randn(20,3).softmax(dim=-1), randint(3, (20,)))) >>> fig_, ax_ = metric.plot(values)

Functional Interface¶
cohen_kappa¶
- torchmetrics.functional.cohen_kappa(preds, target, task, threshold=0.5, num_classes=None, weights=None, ignore_index=None, validate_args=True)[source]¶
Calculate Cohen’s kappa score that measures inter-annotator agreement. It is defined as. :rtype:
Tensor\[\kappa = (p_o - p_e) / (1 - p_e)\]where \(p_o\) is the empirical probability of agreement and \(p_e\) is the expected agreement when both annotators assign labels randomly. Note that \(p_e\) is estimated using a per-annotator empirical prior over the class labels.
This function is a simple wrapper to get the task specific versions of this metric, which is done by setting the
taskargument to either'binary'or'multiclass'. See the documentation ofbinary_cohen_kappa()andmulticlass_cohen_kappa()for the specific details of each argument influence and examples.- Legacy Example:
>>> from torch import tensor >>> target = tensor([1, 1, 0, 0]) >>> preds = tensor([0, 1, 0, 0]) >>> cohen_kappa(preds, target, task="multiclass", num_classes=2) tensor(0.5000)
binary_cohen_kappa¶
- torchmetrics.functional.classification.binary_cohen_kappa(preds, target, threshold=0.5, weights=None, ignore_index=None, validate_args=True)[source]¶
Calculate Cohen’s kappa score that measures inter-annotator agreement for binary tasks.
\[\kappa = (p_o - p_e) / (1 - p_e)\]where \(p_o\) is the empirical probability of agreement and \(p_e\) is the expected agreement when both annotators assign labels randomly. Note that \(p_e\) is estimated using a per-annotator empirical prior over the class labels.
Accepts the following input tensors:
preds(int or float tensor):(N, ...). If preds is a floating point tensor with values outside [0,1] range we consider the input to be logits and will auto apply sigmoid per element. Additionally, we convert to int tensor with thresholding using the value inthreshold.target(int tensor):(N, ...)
Additional dimension
...will be flattened into the batch dimension.- Parameters:
threshold¶ (
float) – Threshold for transforming probability to binary (0,1) predictionsweights¶ (
Optional[Literal['linear','quadratic','none']]) –Weighting type to calculate the score. Choose from:
Noneor'none': no weighting'linear': linear weighting'quadratic': quadratic weighting
ignore_index¶ (
Optional[int]) – Specifies a target value that is ignored and does not contribute to the metric calculationvalidate_args¶ (
bool) – bool indicating if input arguments and tensors should be validated for correctness. Set toFalsefor faster computations.kwargs¶ – Additional keyword arguments, see Advanced metric settings for more info.
- Return type:
- Example (preds is int tensor):
>>> from torch import tensor >>> from torchmetrics.functional.classification import binary_cohen_kappa >>> target = tensor([1, 1, 0, 0]) >>> preds = tensor([0, 1, 0, 0]) >>> binary_cohen_kappa(preds, target) tensor(0.5000)
- Example (preds is float tensor):
>>> from torchmetrics.functional.classification import binary_cohen_kappa >>> target = tensor([1, 1, 0, 0]) >>> preds = tensor([0.35, 0.85, 0.48, 0.01]) >>> binary_cohen_kappa(preds, target) tensor(0.5000)
multiclass_cohen_kappa¶
- torchmetrics.functional.classification.multiclass_cohen_kappa(preds, target, num_classes, weights=None, ignore_index=None, validate_args=True)[source]¶
Calculate Cohen’s kappa score that measures inter-annotator agreement for multiclass tasks.
\[\kappa = (p_o - p_e) / (1 - p_e)\]where \(p_o\) is the empirical probability of agreement and \(p_e\) is the expected agreement when both annotators assign labels randomly. Note that \(p_e\) is estimated using a per-annotator empirical prior over the class labels.
Accepts the following input tensors:
preds:(N, ...)(int tensor) or(N, C, ..)(float tensor). If preds is a floating point we applytorch.argmaxalong theCdimension to automatically convert probabilities/logits into an int tensor.target(int tensor):(N, ...)
Additional dimension
...will be flattened into the batch dimension.- Parameters:
num_classes¶ (
int) – Integer specifying the number of classesweights¶ (
Optional[Literal['linear','quadratic','none']]) –Weighting type to calculate the score. Choose from:
Noneor'none': no weighting'linear': linear weighting'quadratic': quadratic weighting
ignore_index¶ (
Optional[int]) – Specifies a target value that is ignored and does not contribute to the metric calculationvalidate_args¶ (
bool) – bool indicating if input arguments and tensors should be validated for correctness. Set toFalsefor faster computations.kwargs¶ – Additional keyword arguments, see Advanced metric settings for more info.
- Return type:
- Example (pred is integer tensor):
>>> from torch import tensor >>> from torchmetrics.functional.classification import multiclass_cohen_kappa >>> target = tensor([2, 1, 0, 0]) >>> preds = tensor([2, 1, 0, 1]) >>> multiclass_cohen_kappa(preds, target, num_classes=3) tensor(0.6364)
- Example (pred is float tensor):
>>> from torchmetrics.functional.classification import multiclass_cohen_kappa >>> target = tensor([2, 1, 0, 0]) >>> preds = tensor([[0.16, 0.26, 0.58], ... [0.22, 0.61, 0.17], ... [0.71, 0.09, 0.20], ... [0.05, 0.82, 0.13]]) >>> multiclass_cohen_kappa(preds, target, num_classes=3) tensor(0.6364)
