F-Beta Score

Module Interface

class torchmetrics.FBetaScore(**kwargs)

Compute F-score metric.

\[F_{\beta} = (1 + \beta^2) * \frac{\text{precision} * \text{recall}} {(\beta^2 * \text{precision}) + \text{recall}}\]

The metric is only proper defined when \(\text{TP} + \text{FP} \neq 0 \wedge \text{TP} + \text{FN} \neq 0\) where \(\text{TP}\), \(\text{FP}\) and \(\text{FN}\) represent the number of true positives, false positives and false negatives respectively. If this case is encountered for any class/label, the metric for that class/label will be set to zero_division (0 or 1, default is 0) and the overall metric may therefore be affected in turn.

This function is a simple wrapper to get the task specific versions of this metric, which is done by setting the task argument to either 'binary', 'multiclass' or multilabel. See the documentation of BinaryFBetaScore, MulticlassFBetaScore and MultilabelFBetaScore for the specific details of each argument influence and examples.

Legcy Example:

>>> from torch import tensor
>>> target = tensor([0, 1, 2, 0, 1, 2])
>>> preds = tensor([0, 2, 1, 0, 0, 1])
>>> f_beta = FBetaScore(task="multiclass", num_classes=3, beta=0.5)
>>> f_beta(preds, target)
tensor(0.3333)

static __new__(cls, task, beta=1.0, threshold=0.5, num_classes=None, num_labels=None, average='micro', multidim_average='global', top_k=1, ignore_index=None, validate_args=True, zero_division=0, **kwargs)

Initialize task metric.

Return type:

Metric

BinaryFBetaScore

class torchmetrics.classification.BinaryFBetaScore(beta, threshold=0.5, multidim_average='global', ignore_index=None, validate_args=True, zero_division=0, **kwargs)

Compute F-score metric for binary tasks.

\[F_{\beta} = (1 + \beta^2) * \frac{\text{precision} * \text{recall}} {(\beta^2 * \text{precision}) + \text{recall}}\]

The metric is only proper defined when \(\text{TP} + \text{FP} \neq 0 \wedge \text{TP} + \text{FN} \neq 0\) where \(\text{TP}\), \(\text{FP}\) and \(\text{FN}\) represent the number of true positives, false positives and false negatives respectively. If this case is encountered a score of zero_division (0 or 1, default is 0) is returned.

As input to forward and update the metric accepts the following input:

• preds (Tensor): An int tensor or float tensor of shape (N, ...). If preds is a floating point tensor with values outside [0,1] range we consider the input to be logits and will auto apply sigmoid per element. Additionally, we convert to int tensor with thresholding using the value in threshold.

• target (Tensor): An int tensor of shape (N, ...).

As output to forward and compute the metric returns the following output:

• bfbs (Tensor): A tensor whose returned shape depends on the multidim_average argument:

  • If multidim_average is set to global the output will be a scalar tensor

  • If multidim_average is set to samplewise the output will be a tensor of shape (N,) consisting of a scalar value per sample.

If multidim_average is set to samplewise we expect at least one additional dimension ... to be present, which the reduction will then be applied over instead of the sample dimension N.

Parameters:

• beta (float) – Weighting between precision and recall in calculation. Setting to 1 corresponds to equal weight

• threshold (float) – Threshold for transforming probability to binary {0,1} predictions

• multidim_average (Literal['global', 'samplewise']) –

  Defines how additionally dimensions ... should be handled. Should be one of the following:

  • global: Additional dimensions are flatted along the batch dimension

  • samplewise: Statistic will be calculated independently for each sample on the N axis. The statistics in this case are calculated over the additional dimensions.

• ignore_index (Optional[int]) – Specifies a target value that is ignored and does not contribute to the metric calculation

• validate_args (bool) – bool indicating if input arguments and tensors should be validated for correctness. Set to False for faster computations.

• zero_division (float) – Should be 0 or 1. The value returned when \(\text{TP} + \text{FP} = 0 \wedge \text{TP} + \text{FN} = 0\).

Example (preds is int tensor):

>>> from torch import tensor
>>> from torchmetrics.classification import BinaryFBetaScore
>>> target = tensor([0, 1, 0, 1, 0, 1])
>>> preds = tensor([0, 0, 1, 1, 0, 1])
>>> metric = BinaryFBetaScore(beta=2.0)
>>> metric(preds, target)
tensor(0.6667)

Example (preds is float tensor):

>>> from torchmetrics.classification import BinaryFBetaScore
>>> target = tensor([0, 1, 0, 1, 0, 1])
>>> preds = tensor([0.11, 0.22, 0.84, 0.73, 0.33, 0.92])
>>> metric = BinaryFBetaScore(beta=2.0)
>>> metric(preds, target)
tensor(0.6667)

Example (multidim tensors):

>>> from torchmetrics.classification import BinaryFBetaScore
>>> target = tensor([[[0, 1], [1, 0], [0, 1]], [[1, 1], [0, 0], [1, 0]]])
>>> preds = tensor([[[0.59, 0.91], [0.91, 0.99],  [0.63, 0.04]],
...                 [[0.38, 0.04], [0.86, 0.780], [0.45, 0.37]]])
>>> metric = BinaryFBetaScore(beta=2.0, multidim_average='samplewise')
>>> metric(preds, target)
tensor([0.5882, 0.0000])

plot(val=None, ax=None)

Plot a single or multiple values from the metric.

Parameters:

• val (Union[Tensor, Sequence[Tensor], None]) – Either a single result from calling metric.forward or metric.compute or a list of these results. If no value is provided, will automatically call metric.compute and plot that result.

• ax (Optional[Axes]) – An matplotlib axis object. If provided will add plot to that axis

Return type:

tuple[Figure, Union[Axes, ndarray]]

Returns:

Figure object and Axes object

Raises:

ModuleNotFoundError – If matplotlib is not installed

>>> from torch import rand, randint
>>> # Example plotting a single value
>>> from torchmetrics.classification import BinaryFBetaScore
>>> metric = BinaryFBetaScore(beta=2.0)
>>> metric.update(rand(10), randint(2,(10,)))
>>> fig_, ax_ = metric.plot()

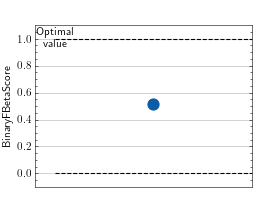
>>> from torch import rand, randint
>>> # Example plotting multiple values
>>> from torchmetrics.classification import BinaryFBetaScore
>>> metric = BinaryFBetaScore(beta=2.0)
>>> values = [ ]
>>> for _ in range(10):
...     values.append(metric(rand(10), randint(2,(10,))))
>>> fig_, ax_ = metric.plot(values)

MulticlassFBetaScore

class torchmetrics.classification.MulticlassFBetaScore(beta, num_classes, top_k=1, average='macro', multidim_average='global', ignore_index=None, validate_args=True, zero_division=0, **kwargs)

Compute F-score metric for multiclass tasks.

\[F_{\beta} = (1 + \beta^2) * \frac{\text{precision} * \text{recall}} {(\beta^2 * \text{precision}) + \text{recall}}\]

The metric is only proper defined when \(\text{TP} + \text{FP} \neq 0 \wedge \text{TP} + \text{FN} \neq 0\) where \(\text{TP}\), \(\text{FP}\) and \(\text{FN}\) represent the number of true positives, false positives and false negatives respectively. If this case is encountered for any class, the metric for that class will be set to zero_division (0 or 1, default is 0) and the overall metric may therefore be affected in turn.

As input to forward and update the metric accepts the following input:

• preds (Tensor): An int tensor of shape (N, ...) or float tensor of shape (N, C, ..). If preds is a floating point we apply torch.argmax along the C dimension to automatically convert probabilities/logits into an int tensor.

• target (Tensor): An int tensor of shape (N, ...).

As output to forward and compute the metric returns the following output:

• mcfbs (Tensor): A tensor whose returned shape depends on the average and multidim_average arguments:

  • If multidim_average is set to global:

    • If average='micro'/'macro'/'weighted', the output will be a scalar tensor

    • If average=None/'none', the shape will be (C,)

  • If multidim_average is set to samplewise:

    • If average='micro'/'macro'/'weighted', the shape will be (N,)

    • If average=None/'none', the shape will be (N, C)

If multidim_average is set to samplewise we expect at least one additional dimension ... to be present, which the reduction will then be applied over instead of the sample dimension N.

Parameters:

• beta (float) – Weighting between precision and recall in calculation. Setting to 1 corresponds to equal weight

• num_classes (int) – Integer specifying the number of classes

• average (Optional[Literal['micro', 'macro', 'weighted', 'none']]) –

  Defines the reduction that is applied over labels. Should be one of the following:

  • micro: Sum statistics over all labels

  • macro: Calculate statistics for each label and average them

  • weighted: calculates statistics for each label and computes weighted average using their support

  • "none" or None: calculates statistic for each label and applies no reduction

• top_k (int) – Number of highest probability or logit score predictions considered to find the correct label. Only works when preds contain probabilities/logits.

• multidim_average (Literal['global', 'samplewise']) –

  Defines how additionally dimensions ... should be handled. Should be one of the following:

  • global: Additional dimensions are flatted along the batch dimension

  • samplewise: Statistic will be calculated independently for each sample on the N axis. The statistics in this case are calculated over the additional dimensions.

• ignore_index (Optional[int]) – Specifies a target value that is ignored and does not contribute to the metric calculation

• validate_args (bool) – bool indicating if input arguments and tensors should be validated for correctness. Set to False for faster computations.

• zero_division (float) – Should be 0 or 1. The value returned when \(\text{TP} + \text{FP} = 0 \wedge \text{TP} + \text{FN} = 0\).

Example (preds is int tensor):

>>> from torch import tensor
>>> from torchmetrics.classification import MulticlassFBetaScore
>>> target = tensor([2, 1, 0, 0])
>>> preds = tensor([2, 1, 0, 1])
>>> metric = MulticlassFBetaScore(beta=2.0, num_classes=3)
>>> metric(preds, target)
tensor(0.7963)
>>> mcfbs = MulticlassFBetaScore(beta=2.0, num_classes=3, average=None)
>>> mcfbs(preds, target)
tensor([0.5556, 0.8333, 1.0000])

Example (preds is float tensor):

>>> from torchmetrics.classification import MulticlassFBetaScore
>>> target = tensor([2, 1, 0, 0])
>>> preds = tensor([[0.16, 0.26, 0.58],
...                 [0.22, 0.61, 0.17],
...                 [0.71, 0.09, 0.20],
...                 [0.05, 0.82, 0.13]])
>>> metric = MulticlassFBetaScore(beta=2.0, num_classes=3)
>>> metric(preds, target)
tensor(0.7963)
>>> mcfbs = MulticlassFBetaScore(beta=2.0, num_classes=3, average=None)
>>> mcfbs(preds, target)
tensor([0.5556, 0.8333, 1.0000])

Example (multidim tensors):

>>> from torchmetrics.classification import MulticlassFBetaScore
>>> target = tensor([[[0, 1], [2, 1], [0, 2]], [[1, 1], [2, 0], [1, 2]]])
>>> preds = tensor([[[0, 2], [2, 0], [0, 1]], [[2, 2], [2, 1], [1, 0]]])
>>> metric = MulticlassFBetaScore(beta=2.0, num_classes=3, multidim_average='samplewise')
>>> metric(preds, target)
tensor([0.4697, 0.2706])
>>> mcfbs = MulticlassFBetaScore(beta=2.0, num_classes=3, multidim_average='samplewise', average=None)
>>> mcfbs(preds, target)
tensor([[0.9091, 0.0000, 0.5000],
        [0.0000, 0.3571, 0.4545]])

plot(val=None, ax=None)

Plot a single or multiple values from the metric.

Parameters:

• val (Union[Tensor, Sequence[Tensor], None]) – Either a single result from calling metric.forward or metric.compute or a list of these results. If no value is provided, will automatically call metric.compute and plot that result.

• ax (Optional[Axes]) – An matplotlib axis object. If provided will add plot to that axis

Return type:

tuple[Figure, Union[Axes, ndarray]]

Returns:

Figure object and Axes object

Raises:

ModuleNotFoundError – If matplotlib is not installed

>>> from torch import randint
>>> # Example plotting a single value per class
>>> from torchmetrics.classification import MulticlassFBetaScore
>>> metric = MulticlassFBetaScore(num_classes=3, beta=2.0, average=None)
>>> metric.update(randint(3, (20,)), randint(3, (20,)))
>>> fig_, ax_ = metric.plot()

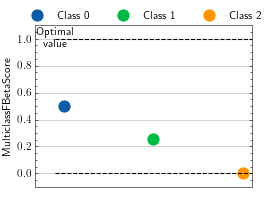
>>> from torch import randint
>>> # Example plotting a multiple values per class
>>> from torchmetrics.classification import MulticlassFBetaScore
>>> metric = MulticlassFBetaScore(num_classes=3, beta=2.0, average=None)
>>> values = []
>>> for _ in range(20):
...     values.append(metric(randint(3, (20,)), randint(3, (20,))))
>>> fig_, ax_ = metric.plot(values)

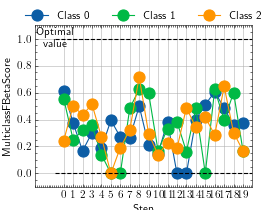
MultilabelFBetaScore

class torchmetrics.classification.MultilabelFBetaScore(beta, num_labels, threshold=0.5, average='macro', multidim_average='global', ignore_index=None, validate_args=True, zero_division=0, **kwargs)

Compute F-score metric for multilabel tasks.

\[F_{\beta} = (1 + \beta^2) * \frac{\text{precision} * \text{recall}} {(\beta^2 * \text{precision}) + \text{recall}}\]

The metric is only proper defined when \(\text{TP} + \text{FP} \neq 0 \wedge \text{TP} + \text{FN} \neq 0\) where \(\text{TP}\), \(\text{FP}\) and \(\text{FN}\) represent the number of true positives, false positives and false negatives respectively. If this case is encountered for any label, the metric for that label will be set to zero_division (0 or 1, default is 0) and the overall metric may therefore be affected in turn.

As input to forward and update the metric accepts the following input:

• preds (Tensor): An int or float tensor of shape (N, C, ...). If preds is a floating point tensor with values outside [0,1] range we consider the input to be logits and will auto apply sigmoid per element. Additionally, we convert to int tensor with thresholding using the value in threshold.

• target (Tensor): An int tensor of shape (N, C, ...).

As output to forward and compute the metric returns the following output:

• mlfbs (Tensor): A tensor whose returned shape depends on the average and multidim_average arguments:

  • If multidim_average is set to global:

    • If average='micro'/'macro'/'weighted', the output will be a scalar tensor

    • If average=None/'none', the shape will be (C,)

  • If multidim_average is set to samplewise:

    • If average='micro'/'macro'/'weighted', the shape will be (N,)

    • If average=None/'none', the shape will be (N, C)

If multidim_average is set to samplewise we expect at least one additional dimension ... to be present, which the reduction will then be applied over instead of the sample dimension N.

Parameters:

• beta (float) – Weighting between precision and recall in calculation. Setting to 1 corresponds to equal weight

• num_labels (int) – Integer specifying the number of labels

• threshold (float) – Threshold for transforming probability to binary (0,1) predictions

• average (Optional[Literal['micro', 'macro', 'weighted', 'none']]) –

  Defines the reduction that is applied over labels. Should be one of the following:

  • micro: Sum statistics over all labels

  • macro: Calculate statistics for each label and average them

  • weighted: calculates statistics for each label and computes weighted average using their support

  • "none" or None: calculates statistic for each label and applies no reduction

• multidim_average (Literal['global', 'samplewise']) –

  Defines how additionally dimensions ... should be handled. Should be one of the following:

  • global: Additional dimensions are flatted along the batch dimension

  • samplewise: Statistic will be calculated independently for each sample on the N axis. The statistics in this case are calculated over the additional dimensions.

• ignore_index (Optional[int]) – Specifies a target value that is ignored and does not contribute to the metric calculation

• validate_args (bool) – bool indicating if input arguments and tensors should be validated for correctness. Set to False for faster computations.

• zero_division (float) – Should be 0 or 1. The value returned when \(\text{TP} + \text{FP} = 0 \wedge \text{TP} + \text{FN} = 0\).

Example (preds is int tensor):

>>> from torch import tensor
>>> from torchmetrics.classification import MultilabelFBetaScore
>>> target = tensor([[0, 1, 0], [1, 0, 1]])
>>> preds = tensor([[0, 0, 1], [1, 0, 1]])
>>> metric = MultilabelFBetaScore(beta=2.0, num_labels=3)
>>> metric(preds, target)
tensor(0.6111)
>>> mlfbs = MultilabelFBetaScore(beta=2.0, num_labels=3, average=None)
>>> mlfbs(preds, target)
tensor([1.0000, 0.0000, 0.8333])

Example (preds is float tensor):

>>> from torchmetrics.classification import MultilabelFBetaScore
>>> target = tensor([[0, 1, 0], [1, 0, 1]])
>>> preds = tensor([[0.11, 0.22, 0.84], [0.73, 0.33, 0.92]])
>>> metric = MultilabelFBetaScore(beta=2.0, num_labels=3)
>>> metric(preds, target)
tensor(0.6111)
>>> mlfbs = MultilabelFBetaScore(beta=2.0, num_labels=3, average=None)
>>> mlfbs(preds, target)
tensor([1.0000, 0.0000, 0.8333])

Example (multidim tensors):

>>> from torchmetrics.classification import MultilabelFBetaScore
>>> target = tensor([[[0, 1], [1, 0], [0, 1]], [[1, 1], [0, 0], [1, 0]]])
>>> preds = tensor([[[0.59, 0.91], [0.91, 0.99],  [0.63, 0.04]],
...                 [[0.38, 0.04], [0.86, 0.780], [0.45, 0.37]]])
>>> metric = MultilabelFBetaScore(num_labels=3, beta=2.0, multidim_average='samplewise')
>>> metric(preds, target)
tensor([0.5556, 0.0000])
>>> mlfbs = MultilabelFBetaScore(num_labels=3, beta=2.0, multidim_average='samplewise', average=None)
>>> mlfbs(preds, target)
tensor([[0.8333, 0.8333, 0.0000],
        [0.0000, 0.0000, 0.0000]])

plot(val=None, ax=None)

Plot a single or multiple values from the metric.

Parameters:

• val (Union[Tensor, Sequence[Tensor], None]) – Either a single result from calling metric.forward or metric.compute or a list of these results. If no value is provided, will automatically call metric.compute and plot that result.

• ax (Optional[Axes]) – An matplotlib axis object. If provided will add plot to that axis

Return type:

tuple[Figure, Union[Axes, ndarray]]

Returns:

Figure and Axes object

Raises:

ModuleNotFoundError – If matplotlib is not installed

>>> from torch import rand, randint
>>> # Example plotting a single value
>>> from torchmetrics.classification import MultilabelFBetaScore
>>> metric = MultilabelFBetaScore(num_labels=3, beta=2.0)
>>> metric.update(randint(2, (20, 3)), randint(2, (20, 3)))
>>> fig_, ax_ = metric.plot()

>>> from torch import rand, randint
>>> # Example plotting multiple values
>>> from torchmetrics.classification import MultilabelFBetaScore
>>> metric = MultilabelFBetaScore(num_labels=3, beta=2.0)
>>> values = [ ]
>>> for _ in range(10):
...     values.append(metric(randint(2, (20, 3)), randint(2, (20, 3))))
>>> fig_, ax_ = metric.plot(values)

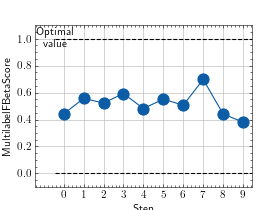
Functional Interface

fbeta_score

torchmetrics.functional.fbeta_score(preds, target, task, beta=1.0, threshold=0.5, num_classes=None, num_labels=None, average='micro', multidim_average='global', top_k=1, ignore_index=None, validate_args=True, zero_division=0)

Compute F-score metric. :rtype: Tensor

\[F_{\beta} = (1 + \beta^2) * \frac{\text{precision} * \text{recall}} {(\beta^2 * \text{precision}) + \text{recall}}\]

This function is a simple wrapper to get the task specific versions of this metric, which is done by setting the task argument to either 'binary', 'multiclass' or multilabel. See the documentation of binary_fbeta_score(), multiclass_fbeta_score() and multilabel_fbeta_score() for the specific details of each argument influence and examples.

Legacy Example:

>>> from torch import tensor
>>> target = tensor([0, 1, 2, 0, 1, 2])
>>> preds = tensor([0, 2, 1, 0, 0, 1])
>>> fbeta_score(preds, target, task="multiclass", num_classes=3, beta=0.5)
tensor(0.3333)

binary_fbeta_score

torchmetrics.functional.classification.binary_fbeta_score(preds, target, beta, threshold=0.5, multidim_average='global', ignore_index=None, validate_args=True, zero_division=0)

Compute F-score metric for binary tasks.

\[F_{\beta} = (1 + \beta^2) * \frac{\text{precision} * \text{recall}} {(\beta^2 * \text{precision}) + \text{recall}}\]

Accepts the following input tensors:

• preds (int or float tensor): (N, ...). If preds is a floating point tensor with values outside [0,1] range we consider the input to be logits and will auto apply sigmoid per element. Additionally, we convert to int tensor with thresholding using the value in threshold.

• target (int tensor): (N, ...)

Parameters:

• preds (Tensor) – Tensor with predictions

• target (Tensor) – Tensor with true labels

• beta (float) – Weighting between precision and recall in calculation. Setting to 1 corresponds to equal weight

• threshold (float) – Threshold for transforming probability to binary {0,1} predictions

• multidim_average (Literal['global', 'samplewise']) –

  Defines how additionally dimensions ... should be handled. Should be one of the following:

  • global: Additional dimensions are flatted along the batch dimension

  • samplewise: Statistic will be calculated independently for each sample on the N axis. The statistics in this case are calculated over the additional dimensions.

• ignore_index (Optional[int]) – Specifies a target value that is ignored and does not contribute to the metric calculation

• validate_args (bool) – bool indicating if input arguments and tensors should be validated for correctness. Set to False for faster computations.

• zero_division (float) – Should be 0 or 1. The value returned when \(\text{TP} + \text{FP} = 0 \wedge \text{TP} + \text{FN} = 0\).

Return type:

Tensor

Returns:

If multidim_average is set to global, the metric returns a scalar value. If multidim_average is set to samplewise, the metric returns (N,) vector consisting of a scalar value per sample.

Example (preds is int tensor):

>>> from torch import tensor
>>> from torchmetrics.functional.classification import binary_fbeta_score
>>> target = tensor([0, 1, 0, 1, 0, 1])
>>> preds = tensor([0, 0, 1, 1, 0, 1])
>>> binary_fbeta_score(preds, target, beta=2.0)
tensor(0.6667)

Example (preds is float tensor):

>>> from torchmetrics.functional.classification import binary_fbeta_score
>>> target = tensor([0, 1, 0, 1, 0, 1])
>>> preds = tensor([0.11, 0.22, 0.84, 0.73, 0.33, 0.92])
>>> binary_fbeta_score(preds, target, beta=2.0)
tensor(0.6667)

Example (multidim tensors):

>>> from torchmetrics.functional.classification import binary_fbeta_score
>>> target = tensor([[[0, 1], [1, 0], [0, 1]], [[1, 1], [0, 0], [1, 0]]])
>>> preds = tensor([[[0.59, 0.91], [0.91, 0.99], [0.63, 0.04]],
...                 [[0.38, 0.04], [0.86, 0.780], [0.45, 0.37]]])
>>> binary_fbeta_score(preds, target, beta=2.0, multidim_average='samplewise')
tensor([0.5882, 0.0000])

multiclass_fbeta_score

torchmetrics.functional.classification.multiclass_fbeta_score(preds, target, beta, num_classes, average='macro', top_k=1, multidim_average='global', ignore_index=None, validate_args=True, zero_division=0)

Compute F-score metric for multiclass tasks.

\[F_{\beta} = (1 + \beta^2) * \frac{\text{precision} * \text{recall}} {(\beta^2 * \text{precision}) + \text{recall}}\]

Accepts the following input tensors:

• preds: (N, ...) (int tensor) or (N, C, ..) (float tensor). If preds is a floating point we apply torch.argmax along the C dimension to automatically convert probabilities/logits into an int tensor.

• target (int tensor): (N, ...)

Parameters:

• preds (Tensor) – Tensor with predictions

• target (Tensor) – Tensor with true labels

• beta (float) – Weighting between precision and recall in calculation. Setting to 1 corresponds to equal weight

• num_classes (int) – Integer specifying the number of classes

• average (Optional[Literal['micro', 'macro', 'weighted', 'none']]) –

  Defines the reduction that is applied over labels. Should be one of the following:

  • micro: Sum statistics over all labels

  • macro: Calculate statistics for each label and average them

  • weighted: calculates statistics for each label and computes weighted average using their support

  • "none" or None: calculates statistic for each label and applies no reduction

• top_k (int) – Number of highest probability or logit score predictions considered to find the correct label. Only works when preds contain probabilities/logits.

• multidim_average (Literal['global', 'samplewise']) –

  Defines how additionally dimensions ... should be handled. Should be one of the following:

  • global: Additional dimensions are flatted along the batch dimension

  • samplewise: Statistic will be calculated independently for each sample on the N axis. The statistics in this case are calculated over the additional dimensions.

• ignore_index (Optional[int]) – Specifies a target value that is ignored and does not contribute to the metric calculation

• validate_args (bool) – bool indicating if input arguments and tensors should be validated for correctness. Set to False for faster computations.

• zero_division (float) – Should be 0 or 1. The value returned when \(\text{TP} + \text{FP} = 0 \wedge \text{TP} + \text{FN} = 0\).

Returns:

• If multidim_average is set to global:

  • If average='micro'/'macro'/'weighted', the output will be a scalar tensor

  • If average=None/'none', the shape will be (C,)

• If multidim_average is set to samplewise:

  • If average='micro'/'macro'/'weighted', the shape will be (N,)

  • If average=None/'none', the shape will be (N, C)

Return type:

The returned shape depends on the average and multidim_average arguments

Example (preds is int tensor):

>>> from torch import tensor
>>> from torchmetrics.functional.classification import multiclass_fbeta_score
>>> target = tensor([2, 1, 0, 0])
>>> preds = tensor([2, 1, 0, 1])
>>> multiclass_fbeta_score(preds, target, beta=2.0, num_classes=3)
tensor(0.7963)
>>> multiclass_fbeta_score(preds, target, beta=2.0, num_classes=3, average=None)
tensor([0.5556, 0.8333, 1.0000])

Example (preds is float tensor):

>>> from torchmetrics.functional.classification import multiclass_fbeta_score
>>> target = tensor([2, 1, 0, 0])
>>> preds = tensor([[0.16, 0.26, 0.58],
...                 [0.22, 0.61, 0.17],
...                 [0.71, 0.09, 0.20],
...                 [0.05, 0.82, 0.13]])
>>> multiclass_fbeta_score(preds, target, beta=2.0, num_classes=3)
tensor(0.7963)
>>> multiclass_fbeta_score(preds, target, beta=2.0, num_classes=3, average=None)
tensor([0.5556, 0.8333, 1.0000])

Example (multidim tensors):

>>> from torchmetrics.functional.classification import multiclass_fbeta_score
>>> target = tensor([[[0, 1], [2, 1], [0, 2]], [[1, 1], [2, 0], [1, 2]]])
>>> preds = tensor([[[0, 2], [2, 0], [0, 1]], [[2, 2], [2, 1], [1, 0]]])
>>> multiclass_fbeta_score(preds, target, beta=2.0, num_classes=3, multidim_average='samplewise')
tensor([0.4697, 0.2706])
>>> multiclass_fbeta_score(preds, target, beta=2.0, num_classes=3, multidim_average='samplewise', average=None)
tensor([[0.9091, 0.0000, 0.5000],
        [0.0000, 0.3571, 0.4545]])

multilabel_fbeta_score

torchmetrics.functional.classification.multilabel_fbeta_score(preds, target, beta, num_labels, threshold=0.5, average='macro', multidim_average='global', ignore_index=None, validate_args=True, zero_division=0)

Compute F-score metric for multilabel tasks.

\[F_{\beta} = (1 + \beta^2) * \frac{\text{precision} * \text{recall}} {(\beta^2 * \text{precision}) + \text{recall}}\]

Accepts the following input tensors:

• preds (int or float tensor): (N, C, ...). If preds is a floating point tensor with values outside [0,1] range we consider the input to be logits and will auto apply sigmoid per element. Additionally, we convert to int tensor with thresholding using the value in threshold.

• target (int tensor): (N, C, ...)

Parameters:

• preds (Tensor) – Tensor with predictions

• target (Tensor) – Tensor with true labels

• beta (float) – Weighting between precision and recall in calculation. Setting to 1 corresponds to equal weight

• num_labels (int) – Integer specifying the number of labels

• threshold (float) – Threshold for transforming probability to binary (0,1) predictions

• average (Optional[Literal['micro', 'macro', 'weighted', 'none']]) –

  Defines the reduction that is applied over labels. Should be one of the following:

  • micro: Sum statistics over all labels

  • macro: Calculate statistics for each label and average them

  • weighted: calculates statistics for each label and computes weighted average using their support

  • "none" or None: calculates statistic for each label and applies no reduction

• multidim_average (Literal['global', 'samplewise']) –

  Defines how additionally dimensions ... should be handled. Should be one of the following:

  • global: Additional dimensions are flatted along the batch dimension

  • samplewise: Statistic will be calculated independently for each sample on the N axis. The statistics in this case are calculated over the additional dimensions.

• ignore_index (Optional[int]) – Specifies a target value that is ignored and does not contribute to the metric calculation

• validate_args (bool) – bool indicating if input arguments and tensors should be validated for correctness. Set to False for faster computations.

• zero_division (float) – Should be 0 or 1. The value returned when \(\text{TP} + \text{FP} = 0 \wedge \text{TP} + \text{FN} = 0\).

Returns:

• If multidim_average is set to global:

  • If average='micro'/'macro'/'weighted', the output will be a scalar tensor

  • If average=None/'none', the shape will be (C,)

• If multidim_average is set to samplewise:

  • If average='micro'/'macro'/'weighted', the shape will be (N,)

  • If average=None/'none', the shape will be (N, C)

Return type:

The returned shape depends on the average and multidim_average arguments

Example (preds is int tensor):

>>> from torch import tensor
>>> from torchmetrics.functional.classification import multilabel_fbeta_score
>>> target = tensor([[0, 1, 0], [1, 0, 1]])
>>> preds = tensor([[0, 0, 1], [1, 0, 1]])
>>> multilabel_fbeta_score(preds, target, beta=2.0, num_labels=3)
tensor(0.6111)
>>> multilabel_fbeta_score(preds, target, beta=2.0, num_labels=3, average=None)
tensor([1.0000, 0.0000, 0.8333])

Example (preds is float tensor):

>>> from torchmetrics.functional.classification import multilabel_fbeta_score
>>> target = tensor([[0, 1, 0], [1, 0, 1]])
>>> preds = tensor([[0.11, 0.22, 0.84], [0.73, 0.33, 0.92]])
>>> multilabel_fbeta_score(preds, target, beta=2.0, num_labels=3)
tensor(0.6111)
>>> multilabel_fbeta_score(preds, target, beta=2.0, num_labels=3, average=None)
tensor([1.0000, 0.0000, 0.8333])

Example (multidim tensors):

>>> from torchmetrics.functional.classification import multilabel_fbeta_score
>>> target = tensor([[[0, 1], [1, 0], [0, 1]], [[1, 1], [0, 0], [1, 0]]])
>>> preds = tensor([[[0.59, 0.91], [0.91, 0.99], [0.63, 0.04]],
...                 [[0.38, 0.04], [0.86, 0.780], [0.45, 0.37]]])
>>> multilabel_fbeta_score(preds, target, num_labels=3, beta=2.0, multidim_average='samplewise')
tensor([0.5556, 0.0000])
>>> multilabel_fbeta_score(preds, target, num_labels=3, beta=2.0, multidim_average='samplewise', average=None)
tensor([[0.8333, 0.8333, 0.0000],
        [0.0000, 0.0000, 0.0000]])