Adjusted Rand Score¶
Module Interface¶
- class torchmetrics.clustering.AdjustedRandScore(**kwargs)[source]¶
Compute Adjusted Rand Score (also known as Adjusted Rand Index).
\[ARS(U, V) = (\text{RS} - \text{Expected RS}) / (\text{Max RS} - \text{Expected RS})\]The adjusted rand score \(\text{ARS}\) is in essence the \(\text{RS}\) (rand score) adjusted for chance. The score ensures that completely randomly cluster labels have a score close to zero and only a perfect match will have a score of 1 (up to a permutation of the labels). The adjusted rand score is symmetric, therefore swapping \(U\) and \(V\) yields the same adjusted rand score.
This clustering metric is an extrinsic measure, because it requires ground truth clustering labels, which may not be available in practice since clustering is generally used for unsupervised learning.
As input to
forwardandupdatethe metric accepts the following input:preds(Tensor): single integer tensor with shape(N,)with predicted cluster labelstarget(Tensor): single integer tensor with shape(N,)with ground truth cluster labels
As output of
forwardandcomputethe metric returns the following output:adj_rand_score(Tensor): Scalar tensor with the adjusted rand score
- Parameters:
kwargs¶ (
Any) – Additional keyword arguments, see Advanced metric settings for more info.
- Example::
>>> import torch >>> from torchmetrics.clustering import AdjustedRandScore >>> metric = AdjustedRandScore() >>> metric(torch.tensor([0, 0, 1, 1]), torch.tensor([0, 0, 1, 1])) tensor(1.) >>> metric(torch.tensor([0, 0, 1, 1]), torch.tensor([0, 1, 0, 1])) tensor(-0.5000)
- plot(val=None, ax=None)[source]¶
Plot a single or multiple values from the metric.
- Parameters:
val¶ (
Union[Tensor,Sequence[Tensor],None]) – Either a single result from calling metric.forward or metric.compute or a list of these results. If no value is provided, will automatically call metric.compute and plot that result.ax¶ (
Optional[Axes]) – An matplotlib axis object. If provided will add plot to that axis
- Return type:
- Returns:
Figure and Axes object
- Raises:
ModuleNotFoundError – If matplotlib is not installed
>>> # Example plotting a single value >>> import torch >>> from torchmetrics.clustering import AdjustedRandScore >>> metric = AdjustedRandScore() >>> metric.update(torch.randint(0, 4, (10,)), torch.randint(0, 4, (10,))) >>> fig_, ax_ = metric.plot(metric.compute())

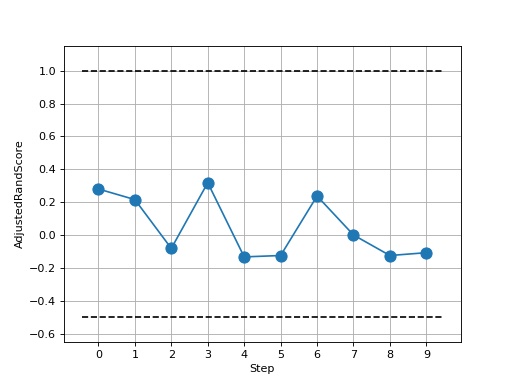
>>> # Example plotting multiple values >>> import torch >>> from torchmetrics.clustering import AdjustedRandScore >>> metric = AdjustedRandScore() >>> values = [ ] >>> for _ in range(10): ... values.append(metric(torch.randint(0, 4, (10,)), torch.randint(0, 4, (10,)))) >>> fig_, ax_ = metric.plot(values)
Functional Interface¶
- torchmetrics.functional.clustering.adjusted_rand_score(preds, target)[source]¶
Compute the Adjusted Rand score between two clusterings.
- Parameters:
- Return type:
- Returns:
Scalar tensor with adjusted rand score
Example
>>> from torchmetrics.functional.clustering import adjusted_rand_score >>> import torch >>> adjusted_rand_score(torch.tensor([0, 0, 1, 1]), torch.tensor([0, 0, 1, 1])) tensor(1.) >>> adjusted_rand_score(torch.tensor([0, 0, 1, 2]), torch.tensor([0, 0, 1, 1])) tensor(0.5714)
