Precision Recall Curve¶
Module Interface¶
- class torchmetrics.PrecisionRecallCurve(**kwargs)[source]¶
Compute the precision-recall curve.
The curve consist of multiple pairs of precision and recall values evaluated at different thresholds, such that the tradeoff between the two values can been seen.
This function is a simple wrapper to get the task specific versions of this metric, which is done by setting the
taskargument to either'binary','multiclass'or'multilabel'. See the documentation ofBinaryPrecisionRecallCurve,MulticlassPrecisionRecallCurveandMultilabelPrecisionRecallCurvefor the specific details of each argument influence and examples.- Legacy Example:
>>> pred = torch.tensor([0, 0.1, 0.8, 0.4]) >>> target = torch.tensor([0, 1, 1, 0]) >>> pr_curve = PrecisionRecallCurve(task="binary") >>> precision, recall, thresholds = pr_curve(pred, target) >>> precision tensor([0.5000, 0.6667, 0.5000, 1.0000, 1.0000]) >>> recall tensor([1.0000, 1.0000, 0.5000, 0.5000, 0.0000]) >>> thresholds tensor([0.0000, 0.1000, 0.4000, 0.8000])
>>> pred = torch.tensor([[0.75, 0.05, 0.05, 0.05, 0.05], ... [0.05, 0.75, 0.05, 0.05, 0.05], ... [0.05, 0.05, 0.75, 0.05, 0.05], ... [0.05, 0.05, 0.05, 0.75, 0.05]]) >>> target = torch.tensor([0, 1, 3, 2]) >>> pr_curve = PrecisionRecallCurve(task="multiclass", num_classes=5) >>> precision, recall, thresholds = pr_curve(pred, target) >>> precision [tensor([0.2500, 1.0000, 1.0000]), tensor([0.2500, 1.0000, 1.0000]), tensor([0.2500, 0.0000, 1.0000]), tensor([0.2500, 0.0000, 1.0000]), tensor([0., 1.])] >>> recall [tensor([1., 1., 0.]), tensor([1., 1., 0.]), tensor([1., 0., 0.]), tensor([1., 0., 0.]), tensor([nan, 0.])] >>> thresholds [tensor([0.0500, 0.7500]), tensor([0.0500, 0.7500]), tensor([0.0500, 0.7500]), tensor([0.0500, 0.7500]), tensor(0.0500)]
BinaryPrecisionRecallCurve¶
- class torchmetrics.classification.BinaryPrecisionRecallCurve(thresholds=None, ignore_index=None, validate_args=True, normalization='sigmoid', **kwargs)[source]¶
Compute the precision-recall curve for binary tasks.
The curve consist of multiple pairs of precision and recall values evaluated at different thresholds, such that the tradeoff between the two values can been seen.
As input to
forwardandupdatethe metric accepts the following input:preds(Tensor): A float tensor of shape(N, ...). Preds should be a tensor containing probabilities or logits for each observation. If preds has values outside [0,1] range we consider the input to be logits and will auto apply sigmoid per element.target(Tensor): An int tensor of shape(N, ...). Target should be a tensor containing ground truth labels, and therefore only contain {0,1} values (except if ignore_index is specified). The value 1 always encodes the positive class.
Tip
Additional dimension
...will be flattened into the batch dimension.As output to
forwardandcomputethe metric returns the following output:precision(Tensor): if thresholds=None a list for each class is returned with an 1d tensor of size(n_thresholds+1, )with precision values (length may differ between classes). If thresholds is set to something else, then a single 2d tensor of size(n_classes, n_thresholds+1)with precision values is returned.recall(Tensor): if thresholds=None a list for each class is returned with an 1d tensor of size(n_thresholds+1, )with recall values (length may differ between classes). If thresholds is set to something else, then a single 2d tensor of size(n_classes, n_thresholds+1)with recall values is returned.thresholds(Tensor): if thresholds=None a list for each class is returned with an 1d tensor of size(n_thresholds, )with increasing threshold values (length may differ between classes). If threshold is set to something else, then a single 1d tensor of size(n_thresholds, )is returned with shared threshold values for all classes.
Note
The implementation both supports calculating the metric in a non-binned but accurate version and a binned version that is less accurate but more memory efficient. Setting the thresholds argument to None will activate the non-binned version that uses memory of size \(\mathcal{O}(n_{samples})\) whereas setting the thresholds argument to either an integer, list or a 1d tensor will use a binned version that uses memory of size \(\mathcal{O}(n_{thresholds})\) (constant memory).
- Parameters:
thresholds¶ (
Union[int,list[float],Tensor,None]) –Can be one of:
If set to None, will use a non-binned approach where thresholds are dynamically calculated from all the data. Most accurate but also most memory consuming approach.
If set to an int (larger than 1), will use that number of thresholds linearly spaced from 0 to 1 as bins for the calculation.
If set to an list of floats, will use the indicated thresholds in the list as bins for the calculation
If set to an 1d tensor of floats, will use the indicated thresholds in the tensor as bins for the calculation.
ignore_index¶ (
Optional[int]) – Specifies a target value that is ignored and does not contribute to the metric calculationvalidate_args¶ (
bool) – bool indicating if input arguments and tensors should be validated for correctness. Set toFalsefor faster computations.normalization¶ (
Optional[Literal['sigmoid','softmax']]) – Specifies a normalization method that is used for batch-wise update regarding negative logits. Set toNoneif negative logits are desired in evaluation.kwargs¶ (
Any) – Additional keyword arguments, see Advanced metric settings for more info.
Example
>>> from torchmetrics.classification import BinaryPrecisionRecallCurve >>> preds = torch.tensor([0, 0.5, 0.7, 0.8]) >>> target = torch.tensor([0, 1, 1, 0]) >>> bprc = BinaryPrecisionRecallCurve(thresholds=None) >>> bprc(preds, target) (tensor([0.5000, 0.6667, 0.5000, 0.0000, 1.0000]), tensor([1.0000, 1.0000, 0.5000, 0.0000, 0.0000]), tensor([0.0000, 0.5000, 0.7000, 0.8000])) >>> bprc = BinaryPrecisionRecallCurve(thresholds=5) >>> bprc(preds, target) (tensor([0.5000, 0.6667, 0.6667, 0.0000, nan, 1.0000]), tensor([1., 1., 1., 0., 0., 0.]), tensor([0.0000, 0.2500, 0.5000, 0.7500, 1.0000]))
- plot(curve=None, score=None, ax=None)[source]¶
Plot a single curve from the metric.
- Parameters:
curve¶ (
Optional[tuple[Tensor,Tensor,Tensor]]) – the output of either metric.compute or metric.forward. If no value is provided, will automatically call metric.compute and plot that result.score¶ (
Union[Tensor,bool,None]) – Provide a area-under-the-curve score to be displayed on the plot. If True and no curve is provided, will automatically compute the score. The score is computed by using the trapezoidal rule to compute the area under the curve.ax¶ (
Optional[Axes]) – An matplotlib axis object. If provided will add plot to that axis
- Return type:
- Returns:
Figure and Axes object
- Raises:
ModuleNotFoundError – If matplotlib is not installed
>>> from torch import rand, randint >>> from torchmetrics.classification import BinaryPrecisionRecallCurve >>> preds = rand(20) >>> target = randint(2, (20,)) >>> metric = BinaryPrecisionRecallCurve() >>> metric.update(preds, target) >>> fig_, ax_ = metric.plot(score=True)
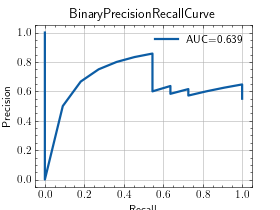
MulticlassPrecisionRecallCurve¶
- class torchmetrics.classification.MulticlassPrecisionRecallCurve(num_classes, thresholds=None, average=None, ignore_index=None, validate_args=True, **kwargs)[source]¶
Compute the precision-recall curve for multiclass tasks.
The curve consist of multiple pairs of precision and recall values evaluated at different thresholds, such that the tradeoff between the two values can been seen.
For multiclass the metric is calculated by iteratively treating each class as the positive class and all other classes as the negative, which is referred to as the one-vs-rest approach. One-vs-one is currently not supported by this metric.
As input to
forwardandupdatethe metric accepts the following input:preds(Tensor): A float tensor of shape(N, C, ...). Preds should be a tensor containing probabilities or logits for each observation. If preds has values outside [0,1] range we consider the input to be logits and will auto apply softmax per sample.target(Tensor): An int tensor of shape(N, ...). Target should be a tensor containing ground truth labels, and therefore only contain values in the [0, n_classes-1] range (except if ignore_index is specified).
Tip
Additional dimension
...will be flattened into the batch dimension.As output to
forwardandcomputethe metric returns the following output:precision(Tensor): A 1d tensor of size(n_thresholds+1, )with precision valuesrecall(Tensor): A 1d tensor of size(n_thresholds+1, )with recall valuesthresholds(Tensor): A 1d tensor of size(n_thresholds, )with increasing threshold values
Note
The implementation both supports calculating the metric in a non-binned but accurate version and a binned version that is less accurate but more memory efficient. Setting the thresholds argument to None will activate the non-binned version that uses memory of size \(\mathcal{O}(n_{samples})\) whereas setting the thresholds argument to either an integer, list or a 1d tensor will use a binned version that uses memory of size \(\mathcal{O}(n_{thresholds} \times n_{classes})\) (constant memory).
- Parameters:
num_classes¶ (
int) – Integer specifying the number of classesthresholds¶ (
Union[int,list[float],Tensor,None]) –Can be one of:
If set to None, will use a non-binned approach where thresholds are dynamically calculated from all the data. Most accurate but also most memory consuming approach.
If set to an int (larger than 1), will use that number of thresholds linearly spaced from 0 to 1 as bins for the calculation.
If set to an list of floats, will use the indicated thresholds in the list as bins for the calculation
If set to a 1D tensor of floats, will use the indicated thresholds in the tensor as bins for the calculation.
average¶ (
Optional[Literal['micro','macro']]) – If aggregation of curves should be applied. By default, the curves are not aggregated and a curve for each class is returned. If average is set to"micro", the metric will aggregate the curves by one hot encoding the targets and flattening the predictions, considering all classes jointly as a binary problem. If average is set to"macro", the metric will aggregate the curves by first interpolating the curves from each class at a combined set of thresholds and then average over the classwise interpolated curves. See averaging curve objects for more info on the different averaging methods.ignore_index¶ (
Optional[int]) – Specifies a target value that is ignored and does not contribute to the metric calculationvalidate_args¶ (
bool) – bool indicating if input arguments and tensors should be validated for correctness. Set toFalsefor faster computations.kwargs¶ (
Any) – Additional keyword arguments, see Advanced metric settings for more info.
Example
>>> from torchmetrics.classification import MulticlassPrecisionRecallCurve >>> preds = torch.tensor([[0.75, 0.05, 0.05, 0.05, 0.05], ... [0.05, 0.75, 0.05, 0.05, 0.05], ... [0.05, 0.05, 0.75, 0.05, 0.05], ... [0.05, 0.05, 0.05, 0.75, 0.05]]) >>> target = torch.tensor([0, 1, 3, 2]) >>> mcprc = MulticlassPrecisionRecallCurve(num_classes=5, thresholds=None) >>> precision, recall, thresholds = mcprc(preds, target) >>> precision [tensor([0.2500, 1.0000, 1.0000]), tensor([0.2500, 1.0000, 1.0000]), tensor([0.2500, 0.0000, 1.0000]), tensor([0.2500, 0.0000, 1.0000]), tensor([0., 1.])] >>> recall [tensor([1., 1., 0.]), tensor([1., 1., 0.]), tensor([1., 0., 0.]), tensor([1., 0., 0.]), tensor([nan, 0.])] >>> thresholds [tensor([0.0500, 0.7500]), tensor([0.0500, 0.7500]), tensor([0.0500, 0.7500]), tensor([0.0500, 0.7500]), tensor(0.0500)] >>> mcprc = MulticlassPrecisionRecallCurve(num_classes=5, thresholds=5) >>> mcprc(preds, target) (tensor([[0.2500, 1.0000, 1.0000, 1.0000, nan, 1.0000], [0.2500, 1.0000, 1.0000, 1.0000, nan, 1.0000], [0.2500, 0.0000, 0.0000, 0.0000, nan, 1.0000], [0.2500, 0.0000, 0.0000, 0.0000, nan, 1.0000], [0.0000, nan, nan, nan, nan, 1.0000]]), tensor([[1., 1., 1., 1., 0., 0.], [1., 1., 1., 1., 0., 0.], [1., 0., 0., 0., 0., 0.], [1., 0., 0., 0., 0., 0.], [nan, nan, nan, nan, nan, 0.]]), tensor([0.0000, 0.2500, 0.5000, 0.7500, 1.0000]))
- plot(curve=None, score=None, ax=None)[source]¶
Plot a single or multiple values from the metric.
- Parameters:
curve¶ (
Union[tuple[Tensor,Tensor,Tensor],tuple[List[Tensor],List[Tensor],List[Tensor]],None]) – the output of either metric.compute or metric.forward. If no value is provided, will automatically call metric.compute and plot that result.score¶ (
Union[Tensor,bool,None]) – Provide a area-under-the-curve score to be displayed on the plot. If True and no curve is provided, will automatically compute the score. The score is computed by using the trapezoidal rule to compute the area under the curve.ax¶ (
Optional[Axes]) – An matplotlib axis object. If provided will add plot to that axis
- Return type:
- Returns:
Figure and Axes object
- Raises:
ModuleNotFoundError – If matplotlib is not installed
>>> from torch import randn, randint >>> from torchmetrics.classification import MulticlassPrecisionRecallCurve >>> preds = randn(20, 3).softmax(dim=-1) >>> target = randint(3, (20,)) >>> metric = MulticlassPrecisionRecallCurve(num_classes=3) >>> metric.update(preds, target) >>> fig_, ax_ = metric.plot(score=True)
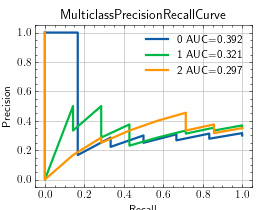
MultilabelPrecisionRecallCurve¶
- class torchmetrics.classification.MultilabelPrecisionRecallCurve(num_labels, thresholds=None, ignore_index=None, validate_args=True, **kwargs)[source]¶
Compute the precision-recall curve for multilabel tasks.
The curve consist of multiple pairs of precision and recall values evaluated at different thresholds, such that the tradeoff between the two values can been seen.
As input to
forwardandupdatethe metric accepts the following input:preds(Tensor): A float tensor of shape(N, C, ...). Preds should be a tensor containing probabilities or logits for each observation. If preds has values outside [0,1] range we consider the input to be logits and will auto apply sigmoid per element.target(Tensor): An int tensor of shape(N, C, ...). Target should be a tensor containing ground truth labels, and therefore only contain {0,1} values (except if ignore_index is specified).
Tip
Additional dimension
...will be flattened into the batch dimension.As output to
forwardandcomputethe metric returns the following a tuple of either 3 tensors or 3 lists containing:precision(TensororList): if thresholds=None a list for each label is returned with an 1d tensor of size(n_thresholds+1, )with precision values (length may differ between labels). If thresholds is set to something else, then a single 2d tensor of size(n_labels, n_thresholds+1)with precision values is returned.recall(TensororList): if thresholds=None a list for each label is returned with an 1d tensor of size(n_thresholds+1, )with recall values (length may differ between labels). If thresholds is set to something else, then a single 2d tensor of size(n_labels, n_thresholds+1)with recall values is returned.thresholds(TensororList): if thresholds=None a list for each label is returned with an 1d tensor of size(n_thresholds, )with increasing threshold values (length may differ between labels). If threshold is set to something else, then a single 1d tensor of size(n_thresholds, )is returned with shared threshold values for all labels.
Note
The implementation both supports calculating the metric in a non-binned but accurate version and a binned version that is less accurate but more memory efficient. Setting the thresholds argument to None will activate the non-binned version that uses memory of size \(\mathcal{O}(n_{samples})\) whereas setting the thresholds argument to either an integer, list or a 1d tensor will use a binned version that uses memory of size \(\mathcal{O}(n_{thresholds} \times n_{labels})\) (constant memory).
- Parameters:
preds¶ – Tensor with predictions
target¶ – Tensor with true labels
thresholds¶ (
Union[int,list[float],Tensor,None]) –Can be one of:
If set to None, will use a non-binned approach where thresholds are dynamically calculated from all the data. Most accurate but also most memory consuming approach.
If set to an int (larger than 1), will use that number of thresholds linearly spaced from 0 to 1 as bins for the calculation.
If set to an list of floats, will use the indicated thresholds in the list as bins for the calculation
If set to an 1d tensor of floats, will use the indicated thresholds in the tensor as bins for the calculation.
ignore_index¶ (
Optional[int]) – Specifies a target value that is ignored and does not contribute to the metric calculationvalidate_args¶ (
bool) – bool indicating if input arguments and tensors should be validated for correctness. Set toFalsefor faster computations.
Example
>>> from torchmetrics.classification import MultilabelPrecisionRecallCurve >>> preds = torch.tensor([[0.75, 0.05, 0.35], ... [0.45, 0.75, 0.05], ... [0.05, 0.55, 0.75], ... [0.05, 0.65, 0.05]]) >>> target = torch.tensor([[1, 0, 1], ... [0, 0, 0], ... [0, 1, 1], ... [1, 1, 1]]) >>> mlprc = MultilabelPrecisionRecallCurve(num_labels=3, thresholds=None) >>> precision, recall, thresholds = mlprc(preds, target) >>> precision [tensor([0.5000, 0.5000, 1.0000, 1.0000]), tensor([0.5000, 0.6667, 0.5000, 0.0000, 1.0000]), tensor([0.7500, 1.0000, 1.0000, 1.0000])] >>> recall [tensor([1.0000, 0.5000, 0.5000, 0.0000]), tensor([1.0000, 1.0000, 0.5000, 0.0000, 0.0000]), tensor([1.0000, 0.6667, 0.3333, 0.0000])] >>> thresholds [tensor([0.0500, 0.4500, 0.7500]), tensor([0.0500, 0.5500, 0.6500, 0.7500]), tensor([0.0500, 0.3500, 0.7500])] >>> mlprc = MultilabelPrecisionRecallCurve(num_labels=3, thresholds=5) >>> mlprc(preds, target) (tensor([[0.5000, 0.5000, 1.0000, 1.0000, nan, 1.0000], [0.5000, 0.6667, 0.6667, 0.0000, nan, 1.0000], [0.7500, 1.0000, 1.0000, 1.0000, nan, 1.0000]]), tensor([[1.0000, 0.5000, 0.5000, 0.5000, 0.0000, 0.0000], [1.0000, 1.0000, 1.0000, 0.0000, 0.0000, 0.0000], [1.0000, 0.6667, 0.3333, 0.3333, 0.0000, 0.0000]]), tensor([0.0000, 0.2500, 0.5000, 0.7500, 1.0000]))
- plot(curve=None, score=None, ax=None)[source]¶
Plot a single or multiple values from the metric.
- Parameters:
curve¶ (
Union[tuple[Tensor,Tensor,Tensor],tuple[List[Tensor],List[Tensor],List[Tensor]],None]) – the output of either metric.compute or metric.forward. If no value is provided, will automatically call metric.compute and plot that result.score¶ (
Union[Tensor,bool,None]) – Provide a area-under-the-curve score to be displayed on the plot. If True and no curve is provided, will automatically compute the score. The score is computed by using the trapezoidal rule to compute the area under the curve.ax¶ (
Optional[Axes]) – An matplotlib axis object. If provided will add plot to that axis
- Return type:
- Returns:
Figure and Axes object
- Raises:
ModuleNotFoundError – If matplotlib is not installed
>>> from torch import rand, randint >>> from torchmetrics.classification import MultilabelPrecisionRecallCurve >>> preds = rand(20, 3) >>> target = randint(2, (20,3)) >>> metric = MultilabelPrecisionRecallCurve(num_labels=3) >>> metric.update(preds, target) >>> fig_, ax_ = metric.plot(score=True)
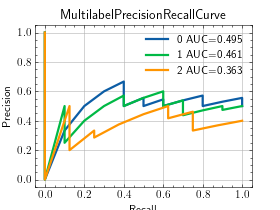
Functional Interface¶
- torchmetrics.functional.precision_recall_curve(preds, target, task, thresholds=None, num_classes=None, num_labels=None, average=None, ignore_index=None, validate_args=True)[source]¶
Compute the precision-recall curve.
The curve consist of multiple pairs of precision and recall values evaluated at different thresholds, such that the tradeoff between the two values can been seen.
This function is a simple wrapper to get the task specific versions of this metric, which is done by setting the
taskargument to either'binary','multiclass'or'multilabel'. See the documentation ofbinary_precision_recall_curve(),multiclass_precision_recall_curve()andmultilabel_precision_recall_curve()for the specific details of each argument influence and examples.- Legacy Example:
>>> pred = torch.tensor([0, 0.1, 0.8, 0.4]) >>> target = torch.tensor([0, 1, 1, 0]) >>> precision, recall, thresholds = precision_recall_curve(pred, target, task='binary') >>> precision tensor([0.5000, 0.6667, 0.5000, 1.0000, 1.0000]) >>> recall tensor([1.0000, 1.0000, 0.5000, 0.5000, 0.0000]) >>> thresholds tensor([0.0000, 0.1000, 0.4000, 0.8000])
>>> pred = torch.tensor([[0.75, 0.05, 0.05, 0.05, 0.05], ... [0.05, 0.75, 0.05, 0.05, 0.05], ... [0.05, 0.05, 0.75, 0.05, 0.05], ... [0.05, 0.05, 0.05, 0.75, 0.05]]) >>> target = torch.tensor([0, 1, 3, 2]) >>> precision, recall, thresholds = precision_recall_curve(pred, target, task='multiclass', num_classes=5) >>> precision [tensor([0.2500, 1.0000, 1.0000]), tensor([0.2500, 1.0000, 1.0000]), tensor([0.2500, 0.0000, 1.0000]), tensor([0.2500, 0.0000, 1.0000]), tensor([0., 1.])] >>> recall [tensor([1., 1., 0.]), tensor([1., 1., 0.]), tensor([1., 0., 0.]), tensor([1., 0., 0.]), tensor([nan, 0.])] >>> thresholds [tensor([0.0500, 0.7500]), tensor([0.0500, 0.7500]), tensor([0.0500, 0.7500]), tensor([0.0500, 0.7500]), tensor([0.0500])]
binary_precision_recall_curve¶
- torchmetrics.functional.classification.binary_precision_recall_curve(preds, target, thresholds=None, ignore_index=None, validate_args=True)[source]¶
Compute the precision-recall curve for binary tasks.
The curve consist of multiple pairs of precision and recall values evaluated at different thresholds, such that the tradeoff between the two values can been seen.
Accepts the following input tensors:
preds(float tensor):(N, ...). Preds should be a tensor containing probabilities or logits for each observation. If preds has values outside [0,1] range we consider the input to be logits and will auto apply sigmoid per element.target(int tensor):(N, ...). Target should be a tensor containing ground truth labels, and therefore only contain {0,1} values (except if ignore_index is specified). The value 1 always encodes the positive class.
Additional dimension
...will be flattened into the batch dimension.The implementation both supports calculating the metric in a non-binned but accurate version and a binned version that is less accurate but more memory efficient. Setting the thresholds argument to None will activate the non-binned version that uses memory of size \(\mathcal{O}(n_{samples})\) whereas setting the thresholds argument to either an integer, list or a 1d tensor will use a binned version that uses memory of size \(\mathcal{O}(n_{thresholds})\) (constant memory).
- Parameters:
thresholds¶ (
Union[int,list[float],Tensor,None]) –Can be one of:
If set to None, will use a non-binned approach where thresholds are dynamically calculated from all the data. Most accurate but also most memory consuming approach.
If set to an int (larger than 1), will use that number of thresholds linearly spaced from 0 to 1 as bins for the calculation.
If set to an list of floats, will use the indicated thresholds in the list as bins for the calculation
If set to an 1d tensor of floats, will use the indicated thresholds in the tensor as bins for the calculation.
ignore_index¶ (
Optional[int]) – Specifies a target value that is ignored and does not contribute to the metric calculationvalidate_args¶ (
bool) – bool indicating if input arguments and tensors should be validated for correctness. Set toFalsefor faster computations.
- Returns:
a tuple of 3 tensors containing:
precision: an 1d tensor of size (n_thresholds+1, ) with precision values
recall: an 1d tensor of size (n_thresholds+1, ) with recall values
thresholds: an 1d tensor of size (n_thresholds, ) with increasing threshold values
- Return type:
(tuple)
Example
>>> from torchmetrics.functional.classification import binary_precision_recall_curve >>> preds = torch.tensor([0, 0.5, 0.7, 0.8]) >>> target = torch.tensor([0, 1, 1, 0]) >>> binary_precision_recall_curve(preds, target, thresholds=None) (tensor([0.5000, 0.6667, 0.5000, 0.0000, 1.0000]), tensor([1.0000, 1.0000, 0.5000, 0.0000, 0.0000]), tensor([0.0000, 0.5000, 0.7000, 0.8000])) >>> binary_precision_recall_curve(preds, target, thresholds=5) (tensor([0.5000, 0.6667, 0.6667, 0.0000, nan, 1.0000]), tensor([1., 1., 1., 0., 0., 0.]), tensor([0.0000, 0.2500, 0.5000, 0.7500, 1.0000]))
multiclass_precision_recall_curve¶
- torchmetrics.functional.classification.multiclass_precision_recall_curve(preds, target, num_classes, thresholds=None, average=None, ignore_index=None, validate_args=True)[source]¶
Compute the precision-recall curve for multiclass tasks.
The curve consist of multiple pairs of precision and recall values evaluated at different thresholds, such that the tradeoff between the two values can been seen.
Accepts the following input tensors:
preds(float tensor):(N, C, ...). Preds should be a tensor containing probabilities or logits for each observation. If preds has values outside [0,1] range we consider the input to be logits and will auto apply softmax per sample.target(int tensor):(N, ...). Target should be a tensor containing ground truth labels, and therefore only contain values in the [0, n_classes-1] range (except if ignore_index is specified).
Additional dimension
...will be flattened into the batch dimension.The implementation both supports calculating the metric in a non-binned but accurate version and a binned version that is less accurate but more memory efficient. Setting the thresholds argument to None will activate the non-binned version that uses memory of size \(\mathcal{O}(n_{samples})\) whereas setting the thresholds argument to either an integer, list or a 1d tensor will use a binned version that uses memory of size \(\mathcal{O}(n_{thresholds} \times n_{classes})\) (constant memory).
- Parameters:
num_classes¶ (
int) – Integer specifying the number of classesthresholds¶ (
Union[int,list[float],Tensor,None]) –Can be one of:
If set to None, will use a non-binned approach where thresholds are dynamically calculated from all the data. Most accurate but also most memory consuming approach.
If set to an int (larger than 1), will use that number of thresholds linearly spaced from 0 to 1 as bins for the calculation.
If set to an list of floats, will use the indicated thresholds in the list as bins for the calculation
If set to an 1d tensor of floats, will use the indicated thresholds in the tensor as bins for the calculation.
average¶ (
Optional[Literal['micro','macro']]) – If aggregation of curves should be applied. By default, the curves are not aggregated and a curve for each class is returned. If average is set to"micro", the metric will aggregate the curves by one hot encoding the targets and flattening the predictions, considering all classes jointly as a binary problem. If average is set to"macro", the metric will aggregate the curves by first interpolating the curves from each class at a combined set of thresholds and then average over the classwise interpolated curves. See averaging curve objects for more info on the different averaging methods.ignore_index¶ (
Optional[int]) – Specifies a target value that is ignored and does not contribute to the metric calculationvalidate_args¶ (
bool) – bool indicating if input arguments and tensors should be validated for correctness. Set toFalsefor faster computations.
- Returns:
a tuple of either 3 tensors or 3 lists containing
precision: if thresholds=None a list for each class is returned with an 1d tensor of size (n_thresholds+1, ) with precision values (length may differ between classes). If thresholds is set to something else, then a single 2d tensor of size (n_classes, n_thresholds+1) with precision values is returned.
recall: if thresholds=None a list for each class is returned with an 1d tensor of size (n_thresholds+1, ) with recall values (length may differ between classes). If thresholds is set to something else, then a single 2d tensor of size (n_classes, n_thresholds+1) with recall values is returned.
thresholds: if thresholds=None a list for each class is returned with an 1d tensor of size (n_thresholds, ) with increasing threshold values (length may differ between classes). If threshold is set to something else, then a single 1d tensor of size (n_thresholds, ) is returned with shared threshold values for all classes.
- Return type:
(tuple)
Example
>>> from torchmetrics.functional.classification import multiclass_precision_recall_curve >>> preds = torch.tensor([[0.75, 0.05, 0.05, 0.05, 0.05], ... [0.05, 0.75, 0.05, 0.05, 0.05], ... [0.05, 0.05, 0.75, 0.05, 0.05], ... [0.05, 0.05, 0.05, 0.75, 0.05]]) >>> target = torch.tensor([0, 1, 3, 2]) >>> precision, recall, thresholds = multiclass_precision_recall_curve( ... preds, target, num_classes=5, thresholds=None ... ) >>> precision [tensor([0.2500, 1.0000, 1.0000]), tensor([0.2500, 1.0000, 1.0000]), tensor([0.2500, 0.0000, 1.0000]), tensor([0.2500, 0.0000, 1.0000]), tensor([0., 1.])] >>> recall [tensor([1., 1., 0.]), tensor([1., 1., 0.]), tensor([1., 0., 0.]), tensor([1., 0., 0.]), tensor([nan, 0.])] >>> thresholds [tensor([0.0500, 0.7500]), tensor([0.0500, 0.7500]), tensor([0.0500, 0.7500]), tensor([0.0500, 0.7500]), tensor([0.0500])] >>> multiclass_precision_recall_curve( ... preds, target, num_classes=5, thresholds=5 ... ) (tensor([[0.2500, 1.0000, 1.0000, 1.0000, nan, 1.0000], [0.2500, 1.0000, 1.0000, 1.0000, nan, 1.0000], [0.2500, 0.0000, 0.0000, 0.0000, nan, 1.0000], [0.2500, 0.0000, 0.0000, 0.0000, nan, 1.0000], [0.0000, nan, nan, nan, nan, 1.0000]]), tensor([[1., 1., 1., 1., 0., 0.], [1., 1., 1., 1., 0., 0.], [1., 0., 0., 0., 0., 0.], [1., 0., 0., 0., 0., 0.], [nan, nan, nan, nan, nan, 0.]]), tensor([0.0000, 0.2500, 0.5000, 0.7500, 1.0000]))
multilabel_precision_recall_curve¶
- torchmetrics.functional.classification.multilabel_precision_recall_curve(preds, target, num_labels, thresholds=None, ignore_index=None, validate_args=True)[source]¶
Compute the precision-recall curve for multilabel tasks.
The curve consist of multiple pairs of precision and recall values evaluated at different thresholds, such that the tradeoff between the two values can been seen.
Accepts the following input tensors:
preds(float tensor):(N, C, ...). Preds should be a tensor containing probabilities or logits for each observation. If preds has values outside [0,1] range we consider the input to be logits and will auto apply sigmoid per element.target(int tensor):(N, C, ...). Target should be a tensor containing ground truth labels, and therefore only contain {0,1} values (except if ignore_index is specified).
Additional dimension
...will be flattened into the batch dimension.The implementation both supports calculating the metric in a non-binned but accurate version and a binned version that is less accurate but more memory efficient. Setting the thresholds argument to None will activate the non-binned version that uses memory of size \(\mathcal{O}(n_{samples})\) whereas setting the thresholds argument to either an integer, list or a 1d tensor will use a binned version that uses memory of size \(\mathcal{O}(n_{thresholds} \times n_{labels})\) (constant memory).
- Parameters:
thresholds¶ (
Union[int,list[float],Tensor,None]) –Can be one of:
If set to None, will use a non-binned approach where thresholds are dynamically calculated from all the data. Most accurate but also most memory consuming approach.
If set to an int (larger than 1), will use that number of thresholds linearly spaced from 0 to 1 as bins for the calculation.
If set to an list of floats, will use the indicated thresholds in the list as bins for the calculation
If set to an 1d tensor of floats, will use the indicated thresholds in the tensor as bins for the calculation.
ignore_index¶ (
Optional[int]) – Specifies a target value that is ignored and does not contribute to the metric calculationvalidate_args¶ (
bool) – bool indicating if input arguments and tensors should be validated for correctness. Set toFalsefor faster computations.
- Returns:
a tuple of either 3 tensors or 3 lists containing
precision: if thresholds=None a list for each label is returned with an 1d tensor of size (n_thresholds+1, ) with precision values (length may differ between labels). If thresholds is set to something else, then a single 2d tensor of size (n_labels, n_thresholds+1) with precision values is returned.
recall: if thresholds=None a list for each label is returned with an 1d tensor of size (n_thresholds+1, ) with recall values (length may differ between labels). If thresholds is set to something else, then a single 2d tensor of size (n_labels, n_thresholds+1) with recall values is returned.
thresholds: if thresholds=None a list for each label is returned with an 1d tensor of size (n_thresholds, ) with increasing threshold values (length may differ between labels). If threshold is set to something else, then a single 1d tensor of size (n_thresholds, ) is returned with shared threshold values for all labels.
- Return type:
(tuple)
Example
>>> from torchmetrics.functional.classification import multilabel_precision_recall_curve >>> preds = torch.tensor([[0.75, 0.05, 0.35], ... [0.45, 0.75, 0.05], ... [0.05, 0.55, 0.75], ... [0.05, 0.65, 0.05]]) >>> target = torch.tensor([[1, 0, 1], ... [0, 0, 0], ... [0, 1, 1], ... [1, 1, 1]]) >>> precision, recall, thresholds = multilabel_precision_recall_curve( ... preds, target, num_labels=3, thresholds=None ... ) >>> precision [tensor([0.5000, 0.5000, 1.0000, 1.0000]), tensor([0.5000, 0.6667, 0.5000, 0.0000, 1.0000]), tensor([0.7500, 1.0000, 1.0000, 1.0000])] >>> recall [tensor([1.0000, 0.5000, 0.5000, 0.0000]), tensor([1.0000, 1.0000, 0.5000, 0.0000, 0.0000]), tensor([1.0000, 0.6667, 0.3333, 0.0000])] >>> thresholds [tensor([0.0500, 0.4500, 0.7500]), tensor([0.0500, 0.5500, 0.6500, 0.7500]), tensor([0.0500, 0.3500, 0.7500])] >>> multilabel_precision_recall_curve( ... preds, target, num_labels=3, thresholds=5 ... ) (tensor([[0.5000, 0.5000, 1.0000, 1.0000, nan, 1.0000], [0.5000, 0.6667, 0.6667, 0.0000, nan, 1.0000], [0.7500, 1.0000, 1.0000, 1.0000, nan, 1.0000]]), tensor([[1.0000, 0.5000, 0.5000, 0.5000, 0.0000, 0.0000], [1.0000, 1.0000, 1.0000, 0.0000, 0.0000, 0.0000], [1.0000, 0.6667, 0.3333, 0.3333, 0.0000, 0.0000]]), tensor([0.0000, 0.2500, 0.5000, 0.7500, 1.0000]))
