Tschuprow’s T¶

Module Interface¶

class torchmetrics.nominal.TschuprowsT(num_classes, bias_correction=True, nan_strategy='replace', nan_replace_value=0.0, **kwargs)[source]¶

Compute Tschuprow’s T statistic measuring the association between two categorical (nominal) data series.

\[T = \sqrt{\frac{\chi^2 / n}{\sqrt{(r - 1) * (k - 1)}}}\]

where

\[\chi^2 = \sum_{i,j} \ frac{\left(n_{ij} - \frac{n_{i.} n_{.j}}{n}\right)^2}{\frac{n_{i.} n_{.j}}{n}}\]

where \(n_{ij}\) denotes the number of times the values \((A_i, B_j)\) are observed with \(A_i, B_j\) represent frequencies of values in preds and target, respectively. Tschuprow’s T is a symmetric coefficient, i.e. \(T(preds, target) = T(target, preds)\), so order of input arguments does not matter. The output values lies in [0, 1] with 1 meaning the perfect association.

As input to forward and update the metric accepts the following input:

preds (Tensor): Either 1D or 2D tensor of categorical (nominal) data from the first data series with shape (batch_size,) or (batch_size, num_classes), respectively.
target (Tensor): Either 1D or 2D tensor of categorical (nominal) data from the second data series with shape (batch_size,) or (batch_size, num_classes), respectively.

As output of forward and compute the metric returns the following output:

tschuprows_t (Tensor): Scalar tensor containing the Tschuprow’s T statistic.

Parameters:

num_classes¶ (int) – Integer specifying the number of classes
bias_correction¶ (bool) – Indication of whether to use bias correction.
nan_strategy¶ (Literal['replace', 'drop']) – Indication of whether to replace or drop NaN values
nan_replace_value¶ (Optional[float]) – Value to replace NaN``s when ``nan_strategy = 'replace'
kwargs¶ (Any) – Additional keyword arguments, see Advanced metric settings for more info.

Raises:

ValueError – If nan_strategy is not one of ‘replace’ and ‘drop’
ValueError – If nan_strategy is equal to ‘replace’ and nan_replace_value is not an int or float

Example:

>>> from torch import randint
>>> from torchmetrics.nominal import TschuprowsT
>>> preds = randint(0, 4, (100,))
>>> target = (preds + torch.randn(100)).round().clamp(0, 4)
>>> tschuprows_t = TschuprowsT(num_classes=5)
>>> tschuprows_t(preds, target)
tensor(0.4930)

plot(val=None, ax=None)[source]¶

Plot a single or multiple values from the metric.

Parameters:

val¶ (Union[Tensor, Sequence[Tensor], None]) – Either a single result from calling metric.forward or metric.compute or a list of these results. If no value is provided, will automatically call metric.compute and plot that result.
ax¶ (Optional[Axes]) – An matplotlib axis object. If provided will add plot to that axis

Return type:

tuple[Figure, Union[Axes, ndarray]]

Returns:

Figure and Axes object

Raises:

ModuleNotFoundError – If matplotlib is not installed

>>> # Example plotting a single value
>>> import torch
>>> from torchmetrics.nominal import TschuprowsT
>>> metric = TschuprowsT(num_classes=5)
>>> metric.update(torch.randint(0, 4, (100,)), torch.randint(0, 4, (100,)))
>>> fig_, ax_ = metric.plot()

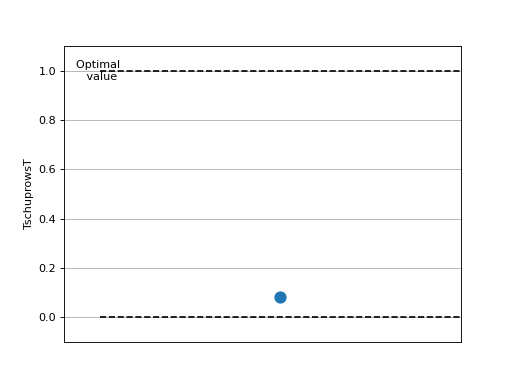
>>> # Example plotting multiple values
>>> import torch
>>> from torchmetrics.nominal import TschuprowsT
>>> metric = TschuprowsT(num_classes=5)
>>> values = [ ]
>>> for _ in range(10):
...     values.append(metric(torch.randint(0, 4, (100,)), torch.randint(0, 4, (100,))))
>>> fig_, ax_ = metric.plot(values)

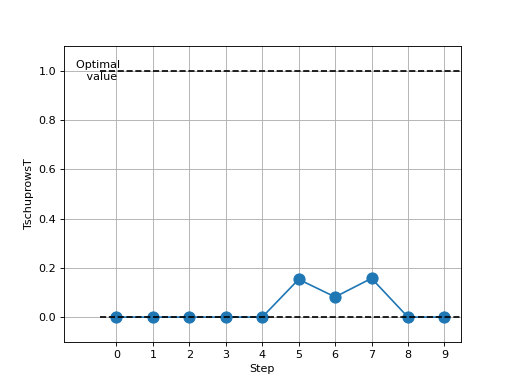
Functional Interface¶

torchmetrics.functional.nominal.tschuprows_t(preds, target, bias_correction=True, nan_strategy='replace', nan_replace_value=0.0)[source]¶

Compute Tschuprow’s T statistic measuring the association between two categorical (nominal) data series.

\[T = \sqrt{\frac{\chi^2 / n}{\sqrt{(r - 1) * (k - 1)}}}\]

where

\[\chi^2 = \sum_{i,j} \ frac{\left(n_{ij} - \frac{n_{i.} n_{.j}}{n}\right)^2}{\frac{n_{i.} n_{.j}}{n}}\]

where \(n_{ij}\) denotes the number of times the values \((A_i, B_j)\) are observed with \(A_i, B_j\) represent frequencies of values in preds and target, respectively.

Tschuprow’s T is a symmetric coefficient, i.e. \(T(preds, target) = T(target, preds)\).

The output values lies in [0, 1] with 1 meaning the perfect association.

Parameters:

preds¶ (Tensor) –
1D or 2D tensor of categorical (nominal) data:
- 1D shape: (batch_size,)
- 2D shape: (batch_size, num_classes)
target¶ (Tensor) –
1D or 2D tensor of categorical (nominal) data:
- 1D shape: (batch_size,)
- 2D shape: (batch_size, num_classes)
bias_correction¶ (bool) – Indication of whether to use bias correction.
nan_strategy¶ (Literal['replace', 'drop']) – Indication of whether to replace or drop NaN values
nan_replace_value¶ (Optional[float]) – Value to replace NaN``s when ``nan_strategy = 'replace'

Return type:

Tensor

Returns:

Tschuprow’s T statistic

Example

>>> from torch import randint, round
>>> from torchmetrics.functional.nominal import tschuprows_t
>>> preds = randint(0, 4, (100,))
>>> target = round(preds + torch.randn(100)).clamp(0, 4)
>>> tschuprows_t(preds, target)
tensor(0.4930)

tschuprows_t_matrix¶

torchmetrics.functional.nominal.tschuprows_t_matrix(matrix, bias_correction=True, nan_strategy='replace', nan_replace_value=0.0)[source]¶

Compute Tschuprow’s T statistic between a set of multiple variables.

This can serve as a convenient tool to compute Tschuprow’s T statistic for analyses of correlation between categorical variables in your dataset.

Parameters:

matrix¶ (Tensor) –
A tensor of categorical (nominal) data, where:
- rows represent a number of data points
- columns represent a number of categorical (nominal) features
bias_correction¶ (bool) – Indication of whether to use bias correction.
nan_strategy¶ (Literal['replace', 'drop']) – Indication of whether to replace or drop NaN values
nan_replace_value¶ (Optional[float]) – Value to replace NaN``s when ``nan_strategy = 'replace'

Return type:

Tensor

Returns:

Tschuprow’s T statistic for a dataset of categorical variables

Example

>>> from torch import randint
>>> from torchmetrics.functional.nominal import tschuprows_t_matrix
>>> matrix = randint(0, 4, (200, 5))
>>> tschuprows_t_matrix(matrix)
tensor([[1.0000, 0.0637, 0.0000, 0.0542, 0.1337],
        [0.0637, 1.0000, 0.0000, 0.0000, 0.0000],
        [0.0000, 0.0000, 1.0000, 0.0000, 0.0649],
        [0.0542, 0.0000, 0.0000, 1.0000, 0.1100],
        [0.1337, 0.0000, 0.0649, 0.1100, 1.0000]])